Experimentelle Untersuchung der Strömungsvorgänge im Simulationsmodell der Silizium-Einkristall-Herstellung nach dem Czochralski-Verfahren

• Einleitung
• Stand der Technik. Literaturübersicht
• Theoretische Grundlagen. Dimensionslose Kennzahlen
• Experimentelle Voraussetzungen
• Darstellung der Ergebnisse
• Schlußbetrachtung und Ausblick
• Literatur

1. Einleitung

Die Anwendung von Einkristallen hat in den vergangenen Jahrzehnten außerordentlich stark zugenommen. Die Qualität dieser Einkristalle wird in erster Linie durch die "Grenzflächen- und Transportphänomene", die während der Herstellung in der Schmelze auftreten, beeinflußt. Ursache für die auftretenden Fluktuationen in der Schmelze sind instationäre Konvektionen, die durch die thermischen und kinematischen Randbedingungen erzeugt werden.

Eine besondere Rolle fällt der Erforschung dieser Konvektionserscheinungen unter verminderter Gravitation, wie z.B. in einem Fallturm, in Parabelflügen oder in einem Weltraumlabor, zu, da sich hier die Grenzflächenkonvektion unabhängig von der natürlichen Konvektion gezielt untersuchen läßt. Hier setzt die vorliegende Arbeit an, die sich mit der Untersuchung von grenzflächenspannungsgetriebenen Konvektionen in einer Czochralski-Konfiguration, womit derzeit etwa 80% der Silizium-Einkristalle weltweit hergestellt werden, experimentell befaßt. Das Ziel dieser Experimente liegt darin, das Zusammenspiel von thermokapillarer, thermischer und erzwungener Konvektion in einer modifizierten Czochralski-Konfiguration zu untersuchen, dabei neue Strömungs-konfigurationen zu entdecken, um daraus wiederum Möglichkeiten zur systematischen Steuerung der Konvektion für die optimale Gestaltung des technischen Prozeßablaufs vorzuschlagen.

2. Stand der Technik. Literaturübersicht

In einem theoretischen Teil dieser Arbeit wurde in einem Literaturüberblick das Umfeld theoretischer und experimenteller Arbeiten zu thermokapillaren Konvektionen im Czochralski-Verfahren, zu Grenzflächenströmungen allgemein und zu Untersuchungen über die Herstellung von Einkristallen nach dem Czochralski-Verfahren beleuchtet, wobei hier ein Auszug wiedergegeben wird.

Mihelcic, Wenzl und Wingerath [1] haben mehrere Arbeiten zu dem Czochralski-Verfahren veröffentlicht. Sie haben die Aussage von Szymczyk [2] bestätigt, daß die Instabilität an der Oberfläche flüssig/gasförmig sofort entsteht, nachdem ein radialer Temperaturgradient an der Grenzfläche der Schmelze erzeugt wird. Des weiteren ist die Instabilität sehr stark von den geometrischen Parametern abhängig.

Müller [3] hat in einer Arbeit aus dem Jahre 1986 geschrieben, daß das Entstehen von makroskopischen Inhomogenitäten weitgehend durch die Stärke und den Verlauf der Konvektionsströmungen in der Schmelze beeinflußt wird. Dagegen wird als Hauptursache der mikroskopischen Inhomogenitäten das instationäre Verhalten der Konvektion angegeben.

In einer numerischen Arbeit über erzwungene Konvektion haben Jaszczur und Szmyd [4] bewiesen, daß die erzwungene Strömung bei einer Oberflächenspannung in einem vertikalen zylindrischen Behälter nicht axialsymmetrisch ist.

Japanische Forscher [5] haben bewiesen, daß die Péclet-Zahl, die dimensionslose Geschwindigkeit der Kristallziehung, bei nichtoszillierenden Oberflächen viel größer ist als bei oszillierenden und die Abweichung zwischen den verschiedenen Zuständen einen hohen Einfluß auf die Länge und den Durchmesser des Kristalls ausübt.

Kanadische und japanische Wissenschaftler [6] haben gemeinsam ein modifiziertes Czochralski-Verfahren entwickelt, wobei sie die derzeit größten Al₂(WO₄)₃ Kristalle gezüchtet haben. Furukawa, Kitamura, Suzuki und Niwa [7] haben LiTaO₃ Monokristalle in einem verdoppelten Schmelztiegel hergestellt.

Die Arbeiten von Duda, Szymczyk, Treuner u.a. [8-17], befaßten sich mit Fragen der Grenzschichtströmung, laminaren und oszillatorischen Strömung, mit der Entwicklung von effizienten optischen Strömungsmeßtechniken zur Untersuchung von thermischen und thermokapillaren Strömungen in verschiedenen geometrischen Konfigurationen sowie thermokapillaren Konvektion in schnell rotierenden Flüssigkeiten.

3. Theoretische Grundlagen. Dimensionslose Kennzahlen

In diesem Kapitel wurden die thermokapillare, thermische und erzwungene Konvektion erläutert. Weiterhin wurden die dimensionslosen Kennzahlen Reynolds-Zahl, Marangoni-Zahl, Prandtl-Zahl, Grashof-Zahl, Bond-Zahl, Rayleigh-Zahl, rotatorische Froude-Zahl, rotatorische Reynolds-Zahl, rotatorische Grashof-Zahl, rotatorische Bond-Zahl und rotatorische Rayleigh-Zahl als Vorschlag zur Analyse der auftretenden Strömung hergeleitet und definiert. Außerdem wurde die charakteristische Geschwindigkeit aus dem Newton´schen Ansatz für die Reibungskräfte zweier Fluidschichten und dem Grenzflächenspannungsgradienten tangential zur ebenen Grenzfläche hergeleitet.

4. Experimentelle Voraussetzungen

Die gesamte Entwicklung der Versuchsanlage von der Planung über Konstruktion, Fertigung, Montage bis hin zur Inbetriebnahme wurde im Rahmen dieser Arbeit an der Fachhochschule Stralsund durchgeführt (siehe Schema in Abb. 1).

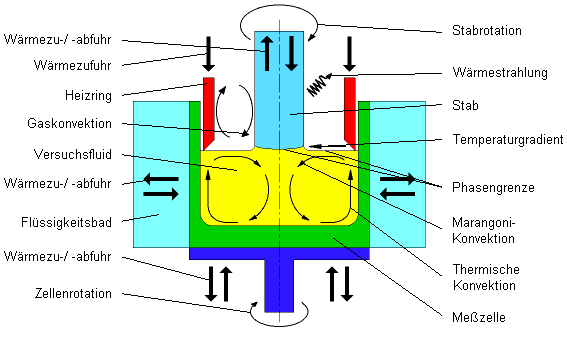
Abb. 1: Schema der modifizierten Czochralski-Konfiguration

Zur Herstellung der thermischen und kinematischen Randbedingungen besteht an der Versuchsanlage die Möglichkeit zur Temperierung von Stab, Flüssigkeitsbad und Meßzellenboden. Weiterhin kann die obere Berandung des Versuchsfluids beheizt werden, was eine Modifikation zum realen Prozeß darstellt. Außerdem können Meßzelle und Stab unabhängig voneinander mit variabler Drehzahl und Drehrichtung rotiert werden.

Zur Visualisierung der Strömungsvorgänge in der Meßzelle wurden zwei optische Meßverfahren simultan eingesetzt (Abb. 2).

Mit Hilfe von Particle Image Thermometry in Verbindung mit Flüssigkristallen wurde das Temperaturfeld qualitativ bestimmt. Mit der Particle Image Velocimetry und den Flüssigkristallen, die hier als Tracer dienen, wurde das Geschwindigkeitsfeld quantitativ ermittelt. Die verwendeten Fluide verhalten sich strömungsmechanisch ähnlich der realen Schmelze, wodurch die Ergebnisse von thermischen und kinematischen Einflüssen bei diesen Versuchen Rückschlüsse auf die Gestaltung des technologischen Prozeßablaufs zulassen.

Die folgende Abbildung gibt die Anordnung der Strömungsmeßtechnik um die Meßzelle wieder.

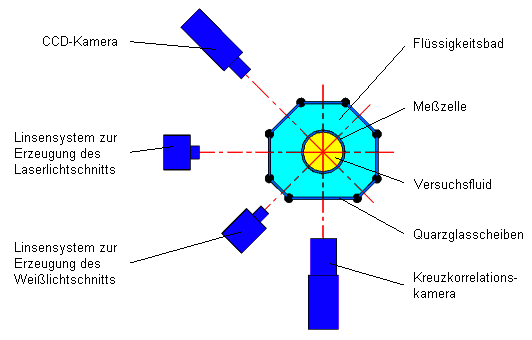
Abb. 2: Anordnung der Lichtschnittverfahren an der Versuchsanlage

5. Darstellung der Ergebnisse

Es wurden 27 grundlegende strömungsmechanische Konfigurationen klassifiziert. Zur übersichtlichen Darstellung der Ergebnisse wurde für jede Konfiguration ein Konfigurationsschema, die eingestellten thermischen und kinematischen Randbedingungen, die sich daraus ergebenden Kennzahlen sowie eine Abbildung des Temperatur-, Strömungs- und Geschwindigkeitsfeldes wiedergegeben. Als Beispiel sei hier eine Konfiguration mit dazugehörigem Strömungsbild sowie Temperatur- und Geschwindigkeitsfeld dargestellt (Abb. 3).

Abb. 3: Konfiguration mit Randbedingungen, Kennzahlen, Temperatur- und Geschwindigkeitsfeld sowie dazugehörigem Strömungsbild

In der Darstellung der instationären Isothermenverläufe wurden die Temperaturfelder der Konfigurationen wiedergegeben (Abb. 4), die bei einem thermisch instationären Zustand aufgenommen wurden. Es wurden einerseits Konfigurationen mit ausschließlich thermischen Randbedingungen (3, 6) und andererseits mit thermischen und kinematischen Randbedingungen (14, 16) dargestellt.

Konfiguration 3	t = t0 + 2 min	t = t0 + 4 min	t = t0 + 8 min
Konfiguration 6	t = t0 + 2 min	t = t0 + 6 min	t = t0 + 10 min
Konfiguration 14	t = t0 + 2 min	t = t0 + 4 min	t = t0 + 7 min
Konfiguration 16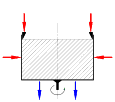	t = t0 + 2 min	t = t0 + 4 min	t = t0 + 7 min

Abb. 4: Instationärer Isothermenverlauf in Abhängigkeit der thermischen und kinematischen Randbedingungen

In der Konfiguration 6 kann man den Einfluß der Marangoni-Zahl auf das Temperaturfeld deutlich sehen. Im Gegensatz zur Konfiguration 3 ist die Grenzflächenkonvektion viel stärker ausgeprägt, die Eindringtiefe der thermokapillaren Strömung ist größer und die Isothermen haben einen ungleichmäßigen Verlauf.

In der Konfiguration 16 kann man den stabilisierenden Einfluß der Rotation auf das Temperaturfeld feststellen. Allerdings muß diese Aussage quantitativ belegt werden.

6. Schlußbetrachtung und Ausblick

Hier wurde ein Resümee über die Arbeit gegeben. Es wurden einige Anregungen zur Optimierung der Versuchsdurchführung und zur Auswertung der Ergebnisse sowie Vorschläge für weitere Versuchsreihen gegeben, wie z.B. Einsatz einer stärkeren Xenon-Impulsentladungslampe zur Optimierung des Weißlichtschnitts, Weiterentwicklung einer Auswertungssoftware für Particle Image Velocimetry, Rechnergesteuerte Auslösung und Speicherung der thermischen und kinematischen Randbedingungen und Bestimmung des Geschwindigkeitsfeldes mit dem Stereoscopic Particle Image Verfahren.

7. Literatur

1. Mihelcic, M.; Wenzl, H.; Wingerath, K.: Flow in Czochralski Crystal Growth Melts, Berichte des Forschungszentrums Jülich, Serie 2697, 1992
2. Szymczyk, J.A.; Chun, Ch.-H.; Siekmann, J.; Wozniak, K.: Liquid Crystal Tracers as a Method for Thermocapillary Flow Diagnostics, Archives of Mechanics, Vol. 41, 2-3, pp. 351-360, 1989
3. Müller, G.: Über die Entstehung von Inhomogenitäten in Halbleitkristallen bei der Herstellung aus Schmelzen, Langensendelbach: Selisch Fachbuch – Verlag, 1986
4. Jaszczur, M.; Szmyd, J. S.: An analysis of buoyancy driven convection in vertical cylinder, Progress in Engineering Heat Transfer, pp. 341-348, IFFM Publishers 1999
5. Hahna, S.; Tsukadaa, T.; Hozawaa, M.; u.a.: Global analysis of heat transfer in Si CZ furnace with specular and diffuse surface, Journal of Crystal Growth, Vol 191 (3), pp. 413-420, 1998
6. Dabkowski, A.; Dabkowska, H. A.; Greedan, J. E., u.a.: Crystal growth of aluminium tungstate Al₂(WO₄)₃ by the Czochralski method from nonstoichiometric melt, Journal of Crystal Growth, Vol 197 (4), pp. 879-882, 1999
7. Furukawa, Y.; Kitamura, K.; Suzuki, E.; Niwa, K.: Stoichiometric LiTaO₃ single crystal by double crucible Czochralski method using automatic powder supply system, Journal of Crystal Growth, Vol 197 (4), pp. 889-895, 1999
8. Duda, U.; Szymczyk, J. A.; Siekmann, J.; Treuner, M.; Delgado, A.; Rath, H. J.: Experimental Investigation of the Influence of the Temperature Gradient on the Thermocapillary Convection in Spherical Drops under Low-Gravity, Proceedings of the European Symposium Fluids in Space, Ajaccio, France, 18-22 November 1991, ESA SP - 353, June 1992
9. Szymczyk, J. A., Siekmann, J.; Ciesliñski, J. T.: Oscillatory Instabilities in a Rapidly Rotating Liquid Annulus, AIAA J. Spacecraft and Rockets , Vol. 29, Nr. 4, pp. 491-497, July - August 1992
10. Szymczyk, J. A.: Influence of the Temperature Gradient on the Oscillatory Instabilities of Thermocapillary Flow at a Rotating Interface, Microgravity Sci. Technol. IV/2, pp. 145-146, 1991
11. Szymczyk, J. A.: Marangoni and Buoyant Convection in a Cylindrical Cell under Normal Gravity, Can. J. Chem.Eng., Vol. 69, pp. 1271-1276, Dec. 1991
12. Szymczyk, J. A.: Thermal and Forced Convection in a Rotating Fluid System, Adv. Space Res. Vol. 11, no. 7, pp. 239-242, 1991
13. Szymczyk, J. A.: Thermokapillare und Zentrifugal-Auftriebskonvektion in schnell rotierenden Fluidsystemen, ZAMM 73, p. 5, 1992
14. Szymczyk, J. A.; Ciesliñski, J. T.; Meironke, H.: Visualisierung der Blasenbildung an einer Kapillare mittels Particle Image Velocimetry, ZAMM, 1999
15. Szymczyk, J. A.; Meironke, H.; Panten, T.: Geschwindigkeits- und Temperaturfeld der Marangoni-Konvektion, ZAMM, 1999
16. Szymczyk, J. A.; Panten, T.: Bestimmung des Geschwindigkeitsfeldes mit Laser-Doppler-Anemometrie im Ventilbereich eines Verbrennungsmotors bei Zylinderentladung, Tagungsband der 4. GALA-Tagung, Lasermethoden in der Strömungsmeßtechnik, Gesellschaft für Laser-Doppler-Anemometrie, Rostock, 12.-14. Sept. 1995
17. Treuner, M.; Delgado, A.; Rath, H. J.; Duda, U.; Szymczyk, J. A.; Siekmann, J.: Experimental Investigation of the Management of Large-Sized Drops and the Onset of Marangoni Convection, Proceedings IUTAM (International Union of Theoretical and Applied Mechanics)- Symposium on Microgravity Fluid Mechanics, Bremen, 1991